第1回:ウォーキングテクニカラー ~ ヒッグス粒子は複合粒子?(2013年5月)
『ヒッグス粒子は複合粒子かもしれません』
2012年、CERN(欧州原子核研究所)で、 126[GeV] 程度の質量でヒッグスと思われる粒子が発見され、素粒子の標準模型を構成する全ての粒子が見つかりました。
しかし、ヒッグス粒子の質量は、理論的には非常に不安定なもので、実験結果をよく説明するには精密な微調整が必要です。これはとても不自然なことで、fine tuningの問題と呼ばれます。
この問題の解決を含め、素粒子の標準模型を超えるいくつかの模型が研究されています。その1つであるウォーキングテクニカラーについて研究されている、KMI理論計算物理室の山崎剛特任助教に、KMIタウレプトン物理グループの青木雅人特任助教と一緒にお話をうかがいました。
ー テクニカラーとは?
『ヒッグス粒子が素粒子ではなく、複合粒子と考える枠組み(模型)のひとつです。』(この枠組みではテクニフェルミオンと呼ばれる新しい素粒子がヒッグス粒子を形成します。)
ー ヒッグス粒子が複合粒子ならば、問題は解決されるのですか?
『より基本的な素粒子の複合粒子だと考えれば、fine tuning の問題はなくなります』しかし、当初提唱されたテクニカラー理論では、予想される複合ヒッグス粒子の質量は1000[Gev]程度と実験と矛盾します。また、実験で分かっている他の色々な事象との整合性が取れません。
ウォーキングテクニカラーによって、実験と矛盾しない結果が得られる!?
ー ウォーキングテクニカラーとは?
『そこで、1986年に、山脇幸一KMI特任教授らが実験と矛盾しない様に拡張された模型、ウォーキングテクニカラーを提唱しました。この模型では、エネルギーが変化しても結合定数がほとんど変化しない(ランニングでなくウォーキングな)領域があります』
ー 複合ヒッグス粒子を形成しているテクニフェルミオンは何種類?
『テク二フェルミオンの種類の数Nf の違いによる、結合定数の変化をみてみましょう』
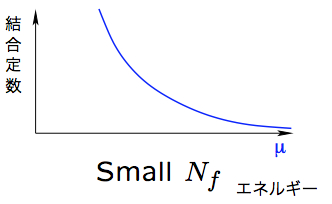
横軸がエネルギー、縦軸が結合定数です。
Nf が2、3個では、結合定数がランニングであることが知られています。(カイラル対称性が自発的に破れる。しかし、ヒッグス粒子の質量が重くなるなど実験と矛盾)
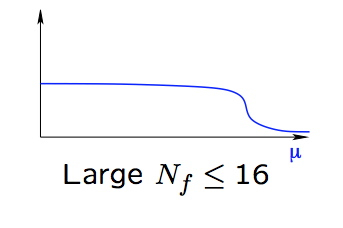
Nf が大きい場合は結合定数は低エネルギーで一定になり、カイラル対称性は自発的に破れません。
ですから、その間あたりで、カイラル対称性が自発的に破れ、かつ、結合定数がウォーキングになると期待されます。
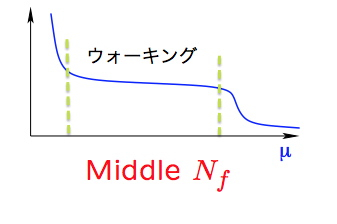
ここで、満たして欲しい性質をまとめておきます。
☆低エネルギーでカイラル対称性が自発的に破れている
☆結合定数がウォーキング
☆ヒッグス粒子の質量が実験と矛盾しないくらい軽い
ー はたして全ての条件を満たす理論はあるのでしょうか?
『非摂動論的な計算で確かめなければなりません』
ー どのような計算なんですか?
『格子ゲージ理論を用います。ヒッグス粒子は一重項スカラー粒子です。格子ゲージ理論の手法でフレーバー1重項スカラー粒子の計算をするのは大変難しく、今まで計算されていませんでした。』
(格子ゲージ理論:1970年代に定式化され、80年に数値計算に成功、その後、計算機と理論との両方の発展により大きな成功を収めてきた計算方法。時空を格子状に区切り数値計算)
ー 1重項スカラー粒子の計算はどのくらい難しいのですか?
『10分の1の計算時間でできる賢い計算方法を利用しても、今までの計算の100倍以上の時間がかかります』なんと、1つの計算プロジェクトに半年~1年もかかるとは、びっくりです。
しかも、山崎さんたちのグループは、別の方法(グルーボール演算子)でも同じ計算をし、結果が同じになることも確かめました。違う計算方法で、結果を比較するのはとても重要ですが、どちらの計算も難しすぎて、今まで比較がありませんでした。
計算の結果、テクニフェルミオンが12種類の場合は、カイラル対称性の自発的な破れがなさそうだとわかってきました。
しかし、テクニフェルミオンが8種類の計算も始められーなんといっても1つの計算に時間がかかるー要求されてる全ての条件が満たされるようだと、大きな期待が持てる結果がでてきています。
もし、ヒッグス粒子が複合粒子ならば、
山崎さん『もちろん、テクニフェルミオンのベクトル粒子も見つかるはずです』
青木雅人さん『どのくらいの質量と予想されていますか?』
山崎さん『誤差が大きいので、まだ、具体的な数字は求められていません』
青木さん『しかし、そういう共同研究もありですね!』

|

|
写真左より、山崎剛さん、木村久美子、青木雅人さん
セミナーのサイトにスライドがあります。



